今回は統計解析で一番出したい結果について勉強していきます

これを出すために色んなルール勉強しました!

そうですね!P値の計算が統計解析のメインです

ぴーち…?は、デザートですよ?

…。それでは統計解析のメインディッシュ、P値を勉強していきましょう!
まずは統計解析の簡単なおさらいから
さぁ、メインディッシュのP値を学ぶ前に、すこしおさらいしておきましょう。
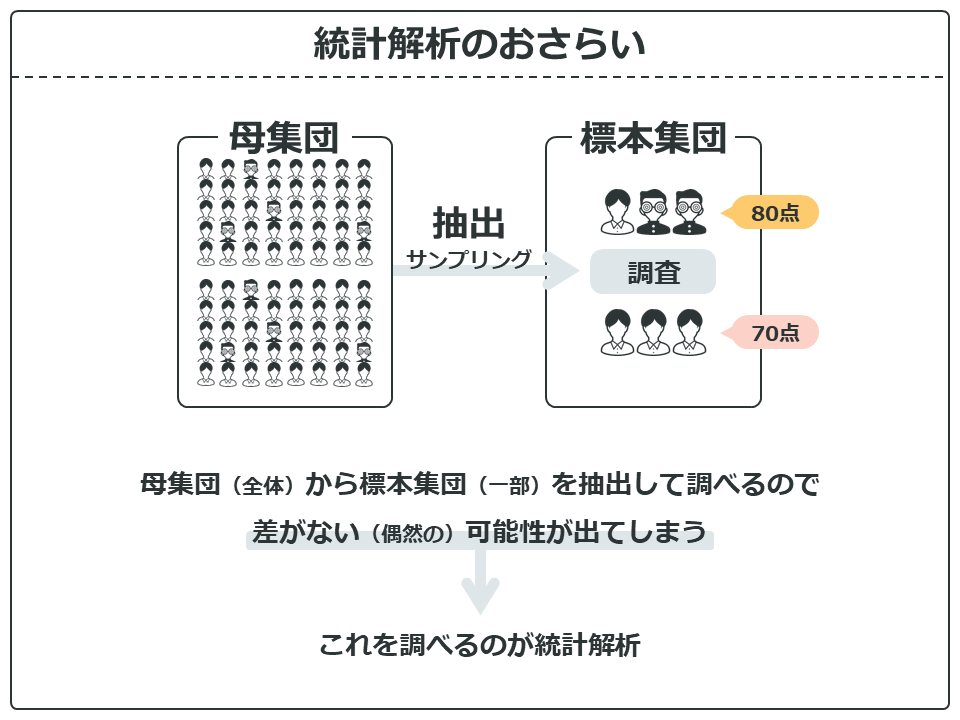
統計解析は、本当は調べたい母集団から、仕方がないので一部を抽出した標本集団を対象に調べるので、差がない(偶然の)可能性が出てしまいます。偶然かどうか調べるのが統計解析でした。
P値って何?何のために計算するの?

偶然というのはつまり確率ですね。統計解析は差がない(偶然の)確率を求めることでした。そして、この差のない確率のことをP値といいます。Pは確率の英語Probabilityの頭文字からとっています。
統計解析において、P値はとっても重要な値です。

では、P値を求めることにどのような意味があるのでしょうか?上の画像をみてイメージしてみましょう。
1組と2組から3人ずつ抽出してのテストの点数を比較したところ、1組が80点、2組が70点で1組のほうがよかったことがわかりました。
でも、2組は納得がいかないですよね。当然「たまたま偶然選んだ3人が頭がイイだけだろ!!」と反論したくなります。
ここでP値の出番です。差がない確率を計算すれば、反対に差がある確率もわかります。差がある確率を示すことができれば、偶然ではないことを示すことができるんですね!結果が偶然ではないことを統計解析により裏付けることができます。
そのため、科学コミュニケーションの場では、統計解析はほとんどの場合必須といえます。
統計解析の流れとP値
では、もう少し形式的に統計解析の流れとP値について見ていきましょう。
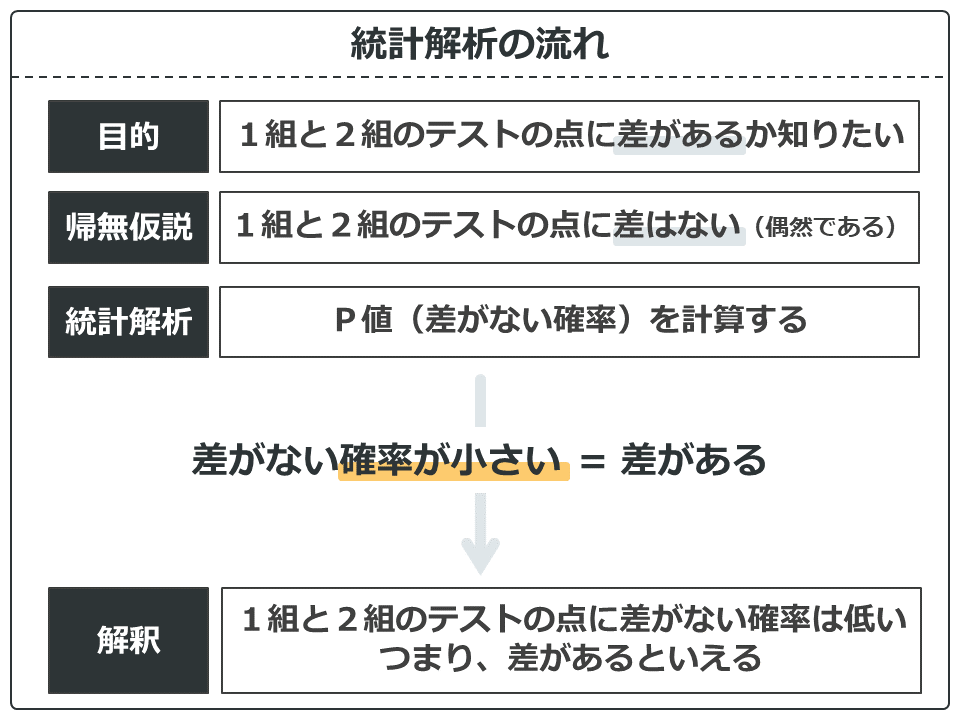
まずは、研究なので目的があります。一般的には差があることを明らかにするのが目的になります。
例えば、「喫煙の有無で将来の肺がん有病率に差があるか知りたい」「リア充と非リア充で友達の数に差があるか知りたい」といった具合です。
そして、「差がある」の目的に対して「差がない」とする帰無仮説を立てます。まぁそういうもんだと思ってください。ちなみに帰無仮説とは本来の目的の反対になるので、無に帰したい、ということで帰無仮説といいます。
そしてこの帰無仮説、つまり差がない確率であるP値を計算します。この差がない確率のP値が小さいことは、反対に差があるということになります。つまりP値が小さい=差があると覚えてください。
なら、最初から差がある確率求めろよって思いますよね?一応、簡単に説明しますが読み飛ばしてもOKです。差がある確率というのは無限にあります。テストの点が80と70なので差は10点の1つしかないようですが、そもそも80点も70点もたまたまの可能性があるので正確ではありません。80.1点かもしれない…と考えると差は無限に考えられます。だから計算できないんですね。一方、差がないというのは差が0ということなので1パターンしかありません。1パターンなら計算できるので、このように差がない確率を求めてから差がある確率を求める方法をとっているわけです。
P値と有意水準について理解しよう

P値が小さいと差があることはわかりましたが、具体的にいくつから小さいといえるのでしょうか?
一般的によく用いられるのはP値5%未満です。つまり、P値を計算して5%未満であれば差があると言っていいよってことです。なにか根拠があるわけではなく、まぁこんくらいならいいよねって感じで決まっています。また、このP値の基準を有意水準と呼びます。研究によってはこの有意水準も1%にしたり、0.01%とかにしたりする場合もありますが、まぁ5%と覚えておきましょう。

P値が計算できれば、統計解析は終わりです。なので結果をまとめることになります。
上の画像では、論文等での表現方法の一例を紹介しています。P値が有意水準未満の場合、有意差ありと表現します。また、有意水準以上であれば、有意差なしと表現します。
表現方法のルールも紹介してありますが、自分の研究分野の論文を真似するのが1番いいですね!論文や学会発表によっては投稿規定などで細かくルールが決められている場合もあるので注意してください。特になければ、上の画像のようなスタイルで記載しておけばいいですね。
P値を扱う上で、知っておかなければならない考え方

さて、P値が有意水準以上(一般的には5%)の場合は、「有意な差は見られなかった」と表現します。しかし、意味合い的には差があるとは今回のデータからではわからないといったニュアンスになります。なので、有意差がないからって「等しい」と結論付けることは普通はしません。
なぜかというと、P値は標本数の大きさにものすごく左右されます。特に小数例での研究ではP値が大きくなりやすいので、そういった場合は標本数を見直してみるといいですね。
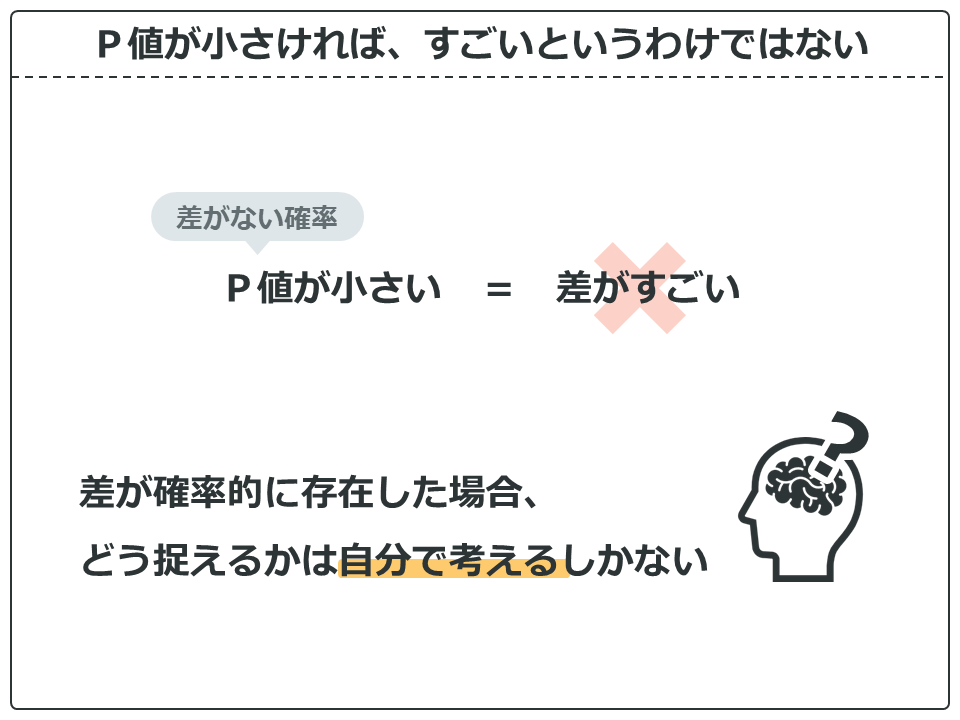
そして、これはぜひ覚えておいてほしいことです。よく間違えている人がいます。
P値というのは差の存在の有無を示しているだけで、その差がすごいということを示しているわけではありません。よく、P値がものすごーく小さい値の結果を、すごい結果だと勘違いする人がいるので気を付けてください。
極端な例ですが、平均体重50kgと平均体重50.1kgでも有意差が出ることはあります。たった100gです。これが1年間のダイエットの効果だとしたら、確かに差はあるのだけれど意味あるの?って思いますよね。
P値が小さく、差が確率的に存在した場合、その差の大きさについてどう捉えるかは、先行研究や臨床的意義を踏まえて自分で考えるしかないんです。本当はこれが研究で1番大切なことです。ついついP値の計算に追われがちですが、結果を捉える目をしっかりと養ってほしいなと思います。
P値はどうやって計算するの?どんな検定手法があるかまとめてみよう
では、P値はどのように計算すればいいのでしょうか?もちろん電卓なんていらないですからね。計算はすべて統計解析に任せます。統計解析のソザイヤサンではExcelと統計ソフトEZRでそれぞれ検定の方法を紹介しています。
また、検定でP値を計算する前に、いくつか統計の基礎知識を知っておく必要があります。
ここまで順番に記事を読んできた人は大丈夫だと思いますが、不安な人は以下のリンクから復習しておきましょう。
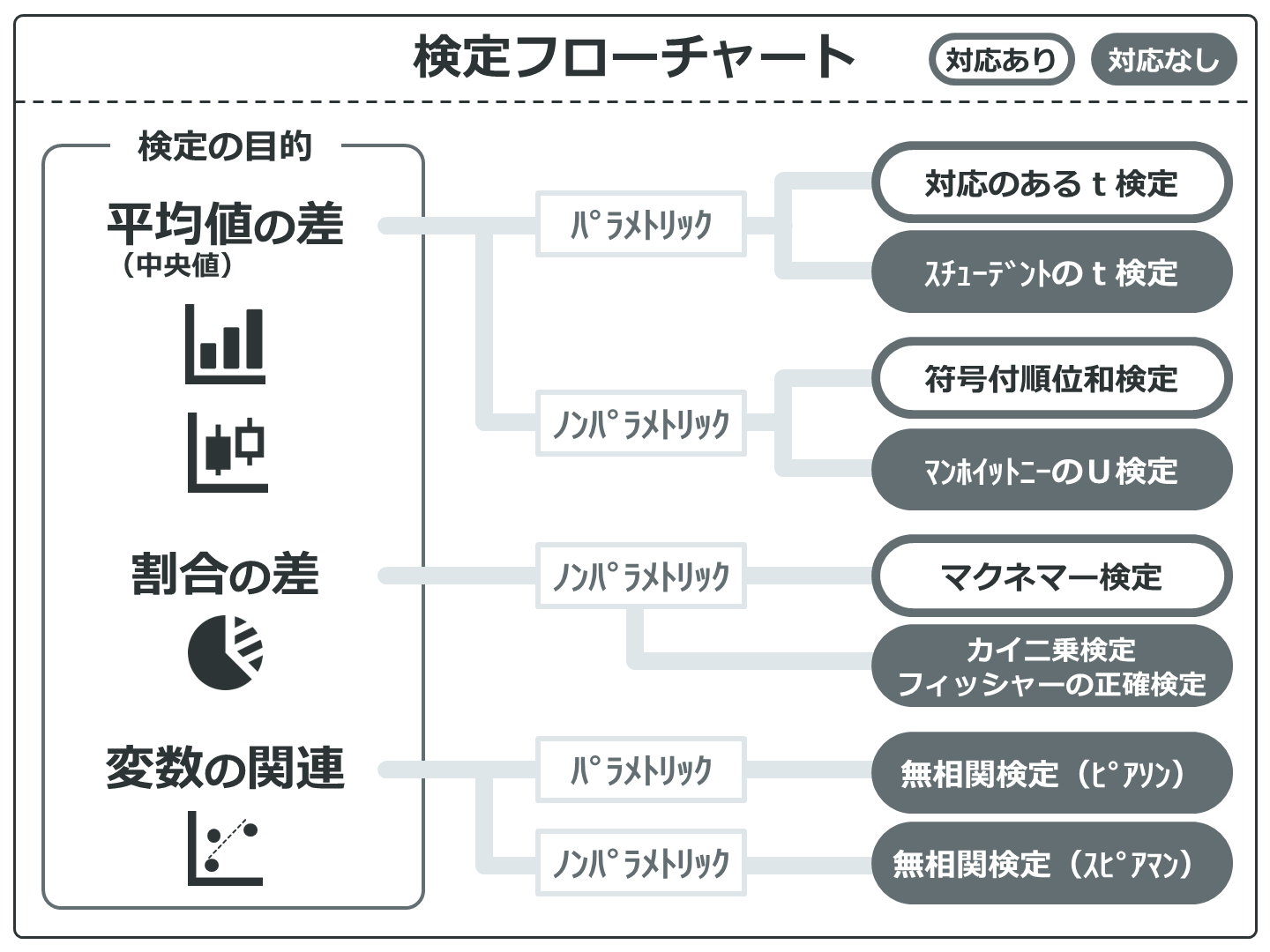
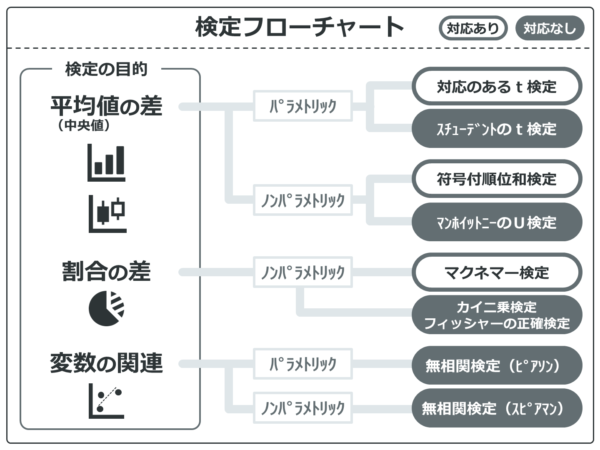
この検定フローチャートに載っている検定は、基本的なものになります。Excelでも統計ソフトEZRでもどちらでもできるように解説していきます。EZRではさらに高度な統計解析についても紹介していきます(Excelではこのくらいが限界です)
またパソコンの人はサイドメニューに、スマホの人はページの一番下のサイドメニューボタンの中に用意しました(スマホは使いにくくてすみません。改善します…たぶん)。
ボタンを押せばいつでもこのフローチャートを見ることができるのでお役立てください。
まとめ(時間がない人はココだけ)
- P値は差がない確率
- P値が5%未満なら有意差あり
- この基準を有意水準という