基本統計量ってなんですか?

変数から計算できる値です

基本なのに何言ってるかよくわからないですね

聞きなれない言葉ですからね。一緒に勉強していきましょう!

キホンをホンキで頑張ります
変数の尺度によって計算できる基本統計量が異なる
基本統計量を学ぶには、必ず変数の尺度(名義尺度、順序尺度、間隔・比例尺度)について知っておく必要があります。ピンとこない人は、次の記事を最初に読んでみてください。
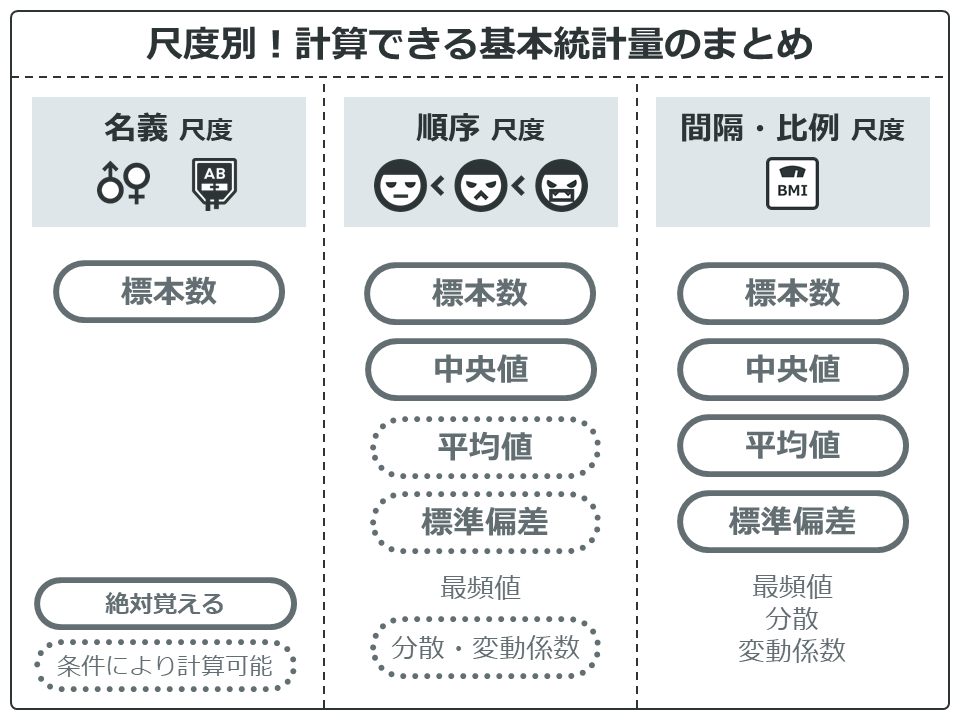
上の画像では、変数の尺度別に計算できる基本統計量がまとまっています。特に太い枠線で囲まれた基本統計量は、統計解析を学ぶ上で必ず知っておく必要があります。
基本統計量とは何か?主要なものについて理解しよう
それではひとつずつ基本統計量を見ていきましょう。Excelで計算する際の関数も一緒に紹介してあるので参考にしてくださいね。
標本数(サンプル数・n数)について
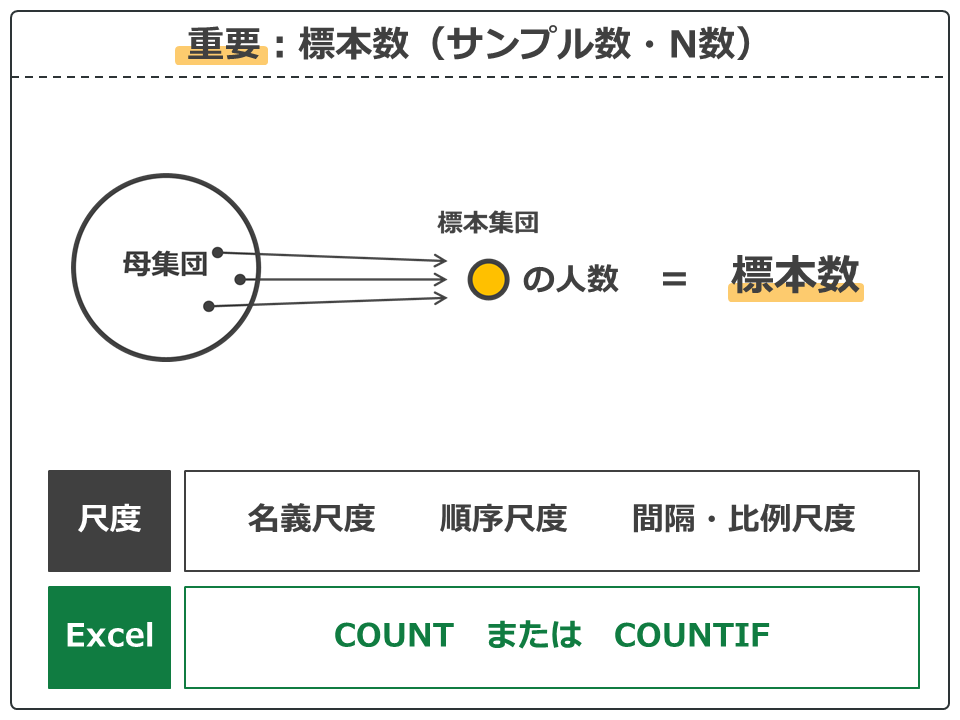
標本数は調査の対象とした標本集団の人数です。もちろんラットや細菌数を対象にした実験でも、その対象にした数が標本数となります。
標本数はサンプル数やn数(NunberのN)とも呼ばれます。論文の表などでは「n=30」といった表記をよく見ますが、これは標本数が30であるという意味です。
単純にデータの数を数えれば計算できるので、どんな尺度の変数でも計算できます。
中央値(メジアン・median)について

データを小さいものから順番に並べて、真ん中にきた値を中央値と呼びます。
順番に並べる必要があるので、大小関係のない名義尺度では計算することができません。
また、順序尺度のデータは本当は四則演算をしてはいけないのですが、データが偶数個で真ん中に2つデータがあるときは、その2つの平均値をとります。
真ん中のデータのことを50%タイル値とも呼びます。中央値=50%タイル値となるということですね。中央値の範囲を示すために中央値と一緒に25%タイル値と75%タイル値(四分位範囲といいます)を併記することがあります。
平均値(ミーン・mean)について

つづいて平均値についてです。こちらは日常生活でもなじみがあるのでわかりやすいですね。あえて説明するなら、データを合計して標本数で割った値となります。
まずここで覚えておいてほしいのは平均値の英語です。平均値はmeanと表記します。Averageではないところが注意委が必要ですね。
基本的には間隔・比例尺度のみで計算できますが、一部の順序尺度でも計算できます。それについては後述します。
なじみやすくわかりやすい平均値ですが、実は平均値には大きな問題が2つ存在しています。
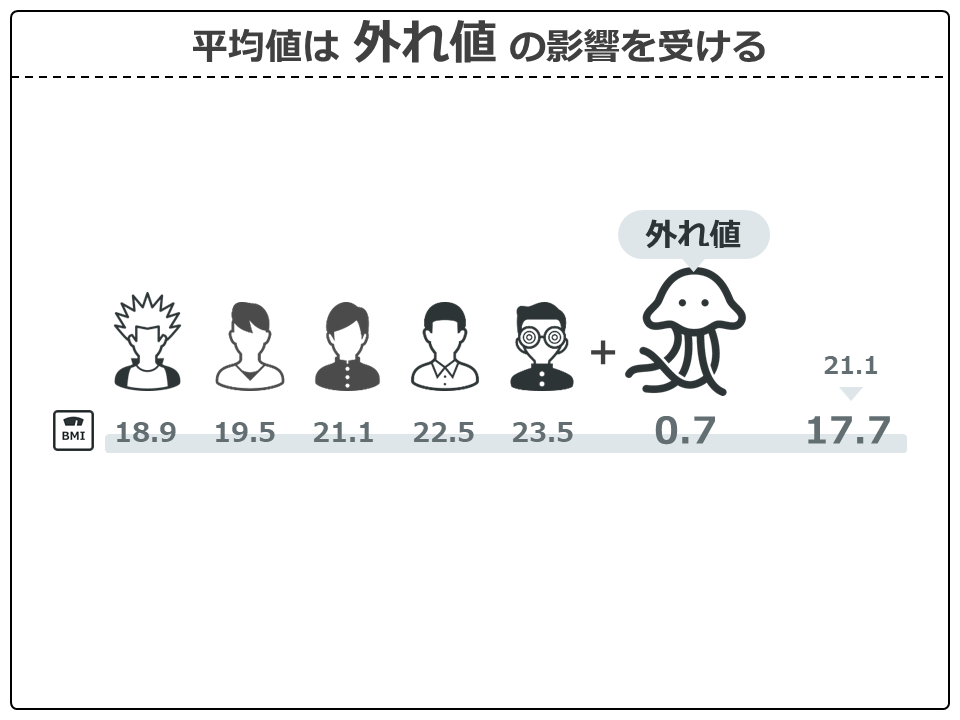
1つめは平均値は外れ値の影響を受ける点です。
男性5人のBMIの平均値は21.1でしたが、そこにとんでもないBMIの火星人が加わることでBMIは17.7になってしまい、大きな影響を受けていることが分かります。
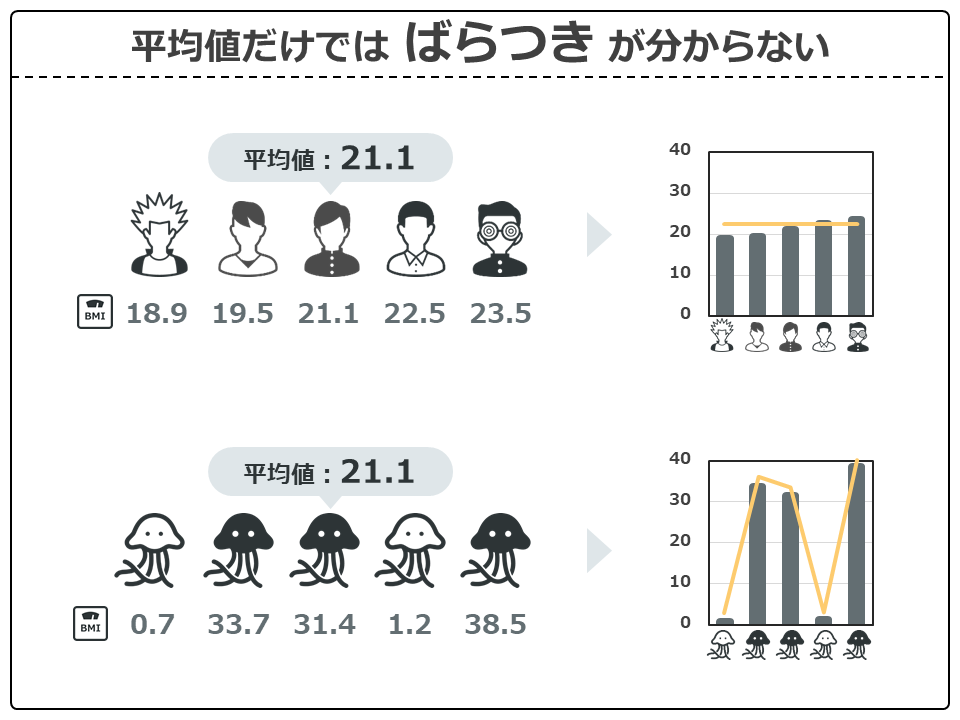
もう1つの問題点は、平均値だけではデータのばらつきが分からない点です。
男性5人と火星人5人のBMIの平均値をそれぞれ計算してみました。どちらも平均値は21.1と同じ値です。
平均値が一緒だから、男性も火星人も同じような集団だねって言えるでしょうか?どう考えてもおかしいですよね。何がおかしいかというと、個別のデータを見ればわかります。グラフにしてみましたがどうですか?
火星人のBMIはバラバラですね。つまり火星人の方がBMIのばらつきが大きいため、おかしかったんですね。
この2つの問題点を解決するために、次に紹介する標準偏差が役に立ちます。
標準偏差(SD:Standard Deviation)について
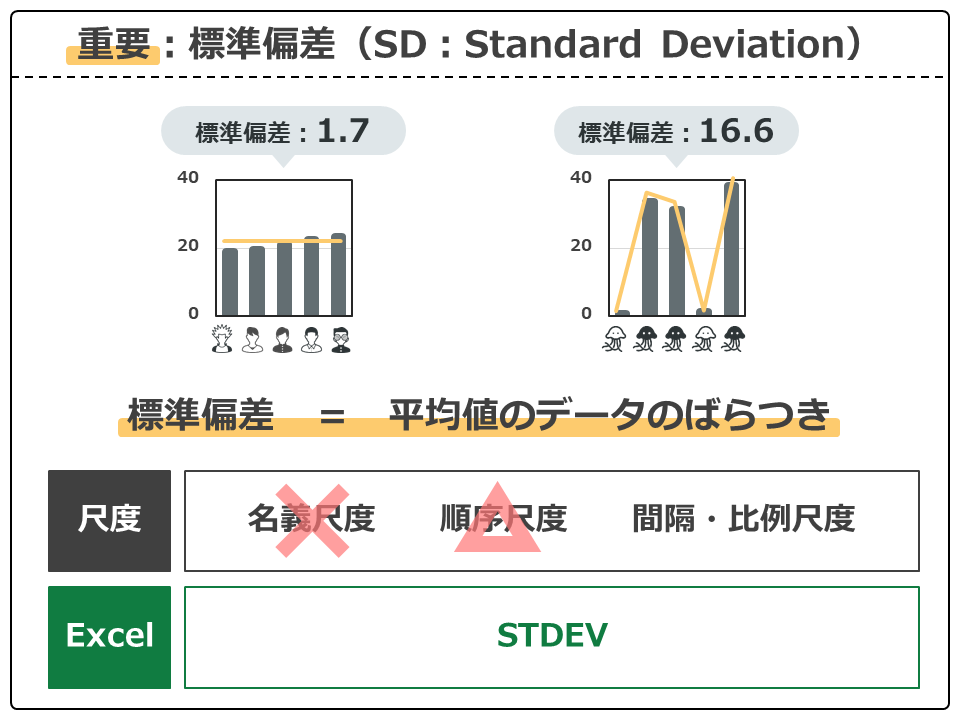
それでは標準偏差についてみていきましょう。聞きなれない言葉ですね。ちょっと難しい基本統計量なので、標準偏差は平均値のデータのばらつきと覚えてください。また論文等ではSDと表記されることがあるので、略称も覚えておきましょう。
それぞれのグラフの上に、計算した標準偏差が記載してあります。男5人は1.7、火星人は16.6です。ちなみに標準偏差の単位は平均値の単位と同じです。つまり、男5人はBMI21.1で1.7のばらつき。火星人はBMI21.1で16.6のばらつきということになります。火星人のばらつきがとても大きいことが数字で表現されていますね!
また、外れ値があるとばらつきも大きくなるので、標準偏差の値も大きくなります。標準偏差が大きな時は、もしかすると外れ値があるかもしれないのでデータを確認してみると良いかもしれません。

もう一歩だけ標準偏差に踏み込んでみましょう。
標準偏差はそれ単品で扱うというよりは、平均値に標準偏差を併記するように使うのが一般的です。そうすることで平均値だけではわからないばらつきをイメージすることができます。
例えば、100人を調査して、年齢が50.0±5.0歳であった場合、45~55歳ぐらいの中年を対象としたんだなと想像がつきます。逆に年齢が50.0±30.0歳であれば、成人から高齢者まで幅広く対象にしたことがイメージできます。
統計学的に言えば(原理は知らなくてOK)、平均±標準偏差の間に、データの68.3%が含まれるとされます。例のように100人を調査して、年齢が50.0±5.0歳であった場合、45~55歳の人が約68人(100人の68.3%)いるということになります。
同じように2倍の標準偏差の範囲に95.4%(例でいえば40~60歳の範囲に約95人)、3倍の標準偏差の範囲に99.7%(例でいえば35~65歳の範囲に約99~100人)が含まれるということになります。統計って不思議ですね!
順序尺度で計算できる基本統計量について

後回しにしていた、平均値や標準偏差で順序尺度が△だった理由を説明します。
まず、原則として順序尺度は大小関係しかわからないので、値を出すために四則演算(+-×÷)が必要な平均値や標準偏差といった基本統計量は計算できません。
しかし、条件によっては間隔・比例尺度として扱うことができる場合があります。
条件としては5つ以上の選択肢があり、中央の選択肢を中心に左右対称になっている場合です。画像の例を見てもらうとわかりますが、中央の「どちらともいえない」を中心に左右対称になっています。
一方、2つめの例の場合、左右対称でない場合や選択肢が3つと少ないときは、順序尺度として扱うようにしましょう。
その他の基本統計量について

最後に、その他の基本統計量についてもまとめておきます。名前くらいは知っておいてもいいかもしれないですね。
まとめ(時間がない人はココだけ)
基本統計量は統計解析を行う上で必ず必要になります。しっかりと勉強しておきましょう。
以下の記事から、Excelのデータを使って実際に計算してみることができるのでぜひ挑戦してみてください。
- 標本数:対象者の数
- 中央値:順番に並べた真ん中
- 平均値:ばらつきを示せない
- 標準偏差:平均値のデータのばらつき