えっと、そもそも統計解析ってなんですか?

確かに、知らない人からするとまず何をするものかもわからないですね

そうなんです。なんか難しそうなイメージはありますけど。

まずはザックリと、統計解析で何ができるか見ていきましょう
統計解析。その前に…
さて、統計解析といわれると難しいイメージがあると思います。確かに統計解析の原理はとても難しく、私自身も全部を把握するなんて到底無理だと思っています。
統計解析の前に、まずは下の画像を見てみましょう。
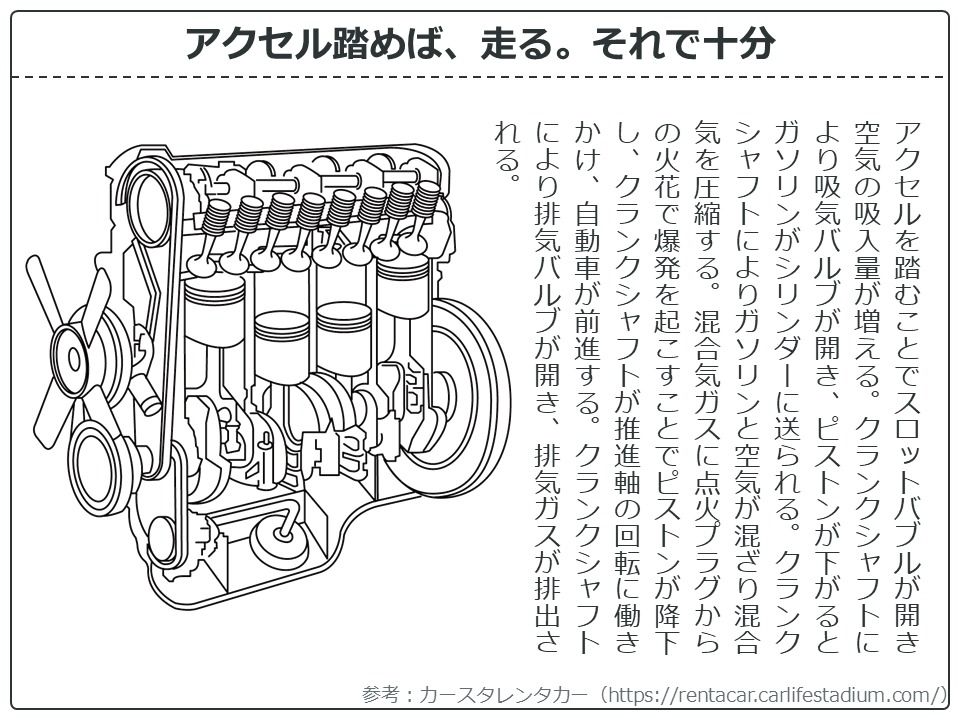
アクセルを踏むと、なぜ車は走るのか知っていますか?知らなくても私たちは普通に車に乗って運転することができていますよね。
統計解析だって同じことなんです。

これはよく使う統計解析方法の計算式です。意味わからないですよね。でも、おそらくほとんどすべての統計解析をする人は、統計解析をする際にこの式を使いません。
なぜなら、パソコンでマウスをポチポチ、キーボードをカタカタするだけで答えは出るからです。
車と同じ。アクセルを踏めば走る。統計解析も、ポチポチすれば答えがでます。もちろん仕組みを知っておくに越したことはないですけどね。
でも、車の運転には交通ルールを覚えなければいけません。交通ルールを知らずに運転したらどうなるかわかりますよね?
統計解析をポチポチするためにも、最低限のルールを覚える必要があります。そうしないと事故を起こしてしまします。
この記事で、統計解析で何ができるかなんとなくわかったら、次は最低限のルールを学んできましょう。
統計解析は、どんな時に必要なのか?
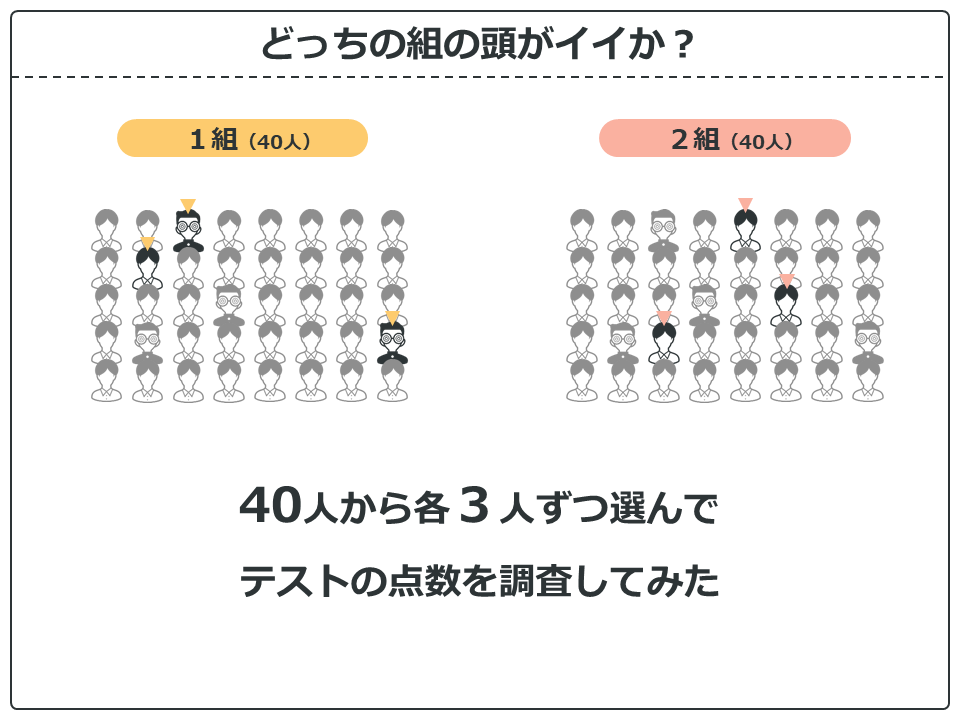
さて、では統計解析はどんな時に必要になるのでしょう?
1組と2組の40人の学生の中からそれぞれ3人ずつ選んで、テストの点数を調査してみました。
そうするとこのような結果でした。
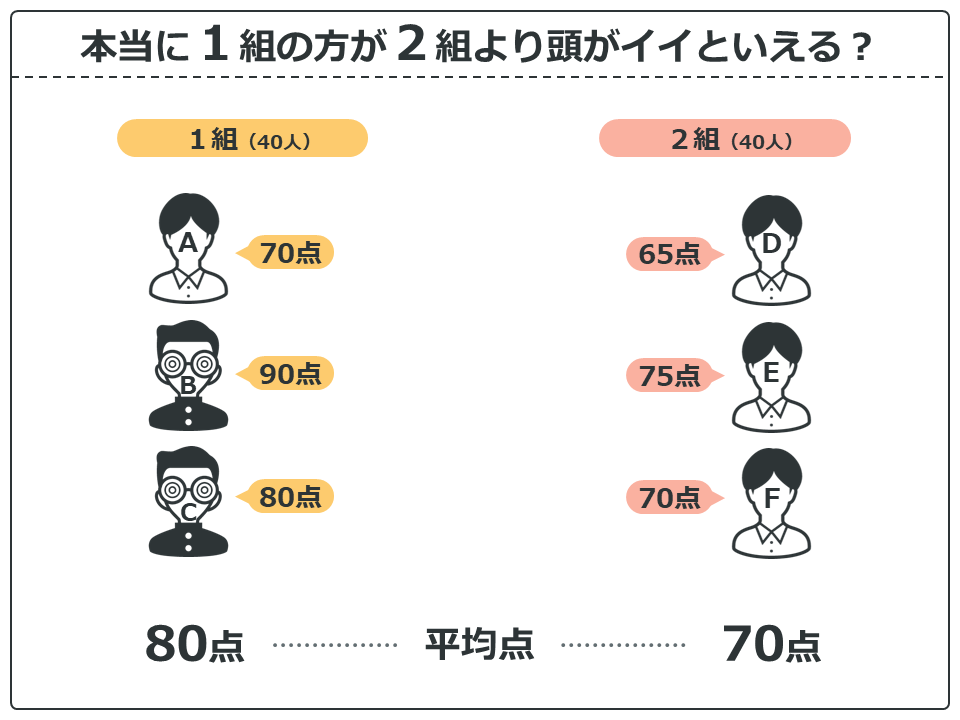
結果を見てみると、1組のテストの平均点は80点、2組は70点となっています。どうやら1組の方が頭がイイように思いますが本当にそうでしょうか?
何か違和感がありますよね…この違和感、統計解析においてとっても大事なことなんです。
では、それぞれの組の意見を聞いてみましょう。
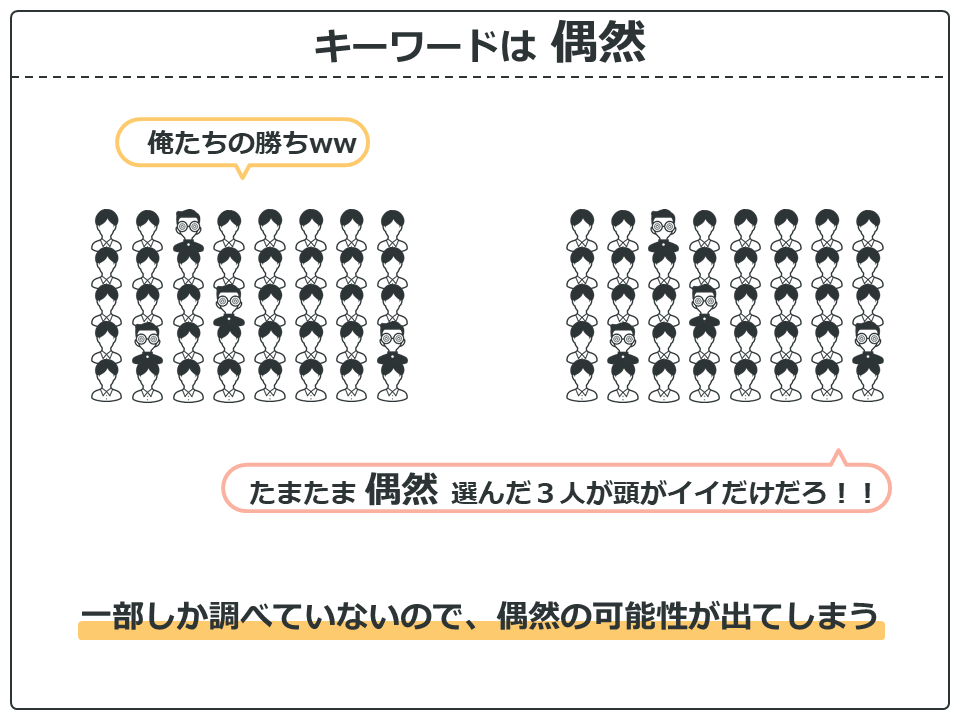
違和感の正体は、2組の学生の意見の通りですね。40人の組からたった3人選んで調べただけでは、たまたま偶然ということが起きてもおかしくないと思いませんか?
一部しか調べていないので、偶然の可能性が出てしまうのですね。もちろん全員調べることができれば真実がハッキリします。
しかし、現実の世界において例えば「東京都と大阪府の中学生のテストの平均値を比較したい」といっても、全員調べることは難しいので、一部を調べることになります。そうすると偶然の可能性が出てきてしまいます。
統計解析は、偶然かどうか確かめるために必要なツールなのです。
- 偶然かどうか確かめるために必要
統計解析で、どんなことができるのか?
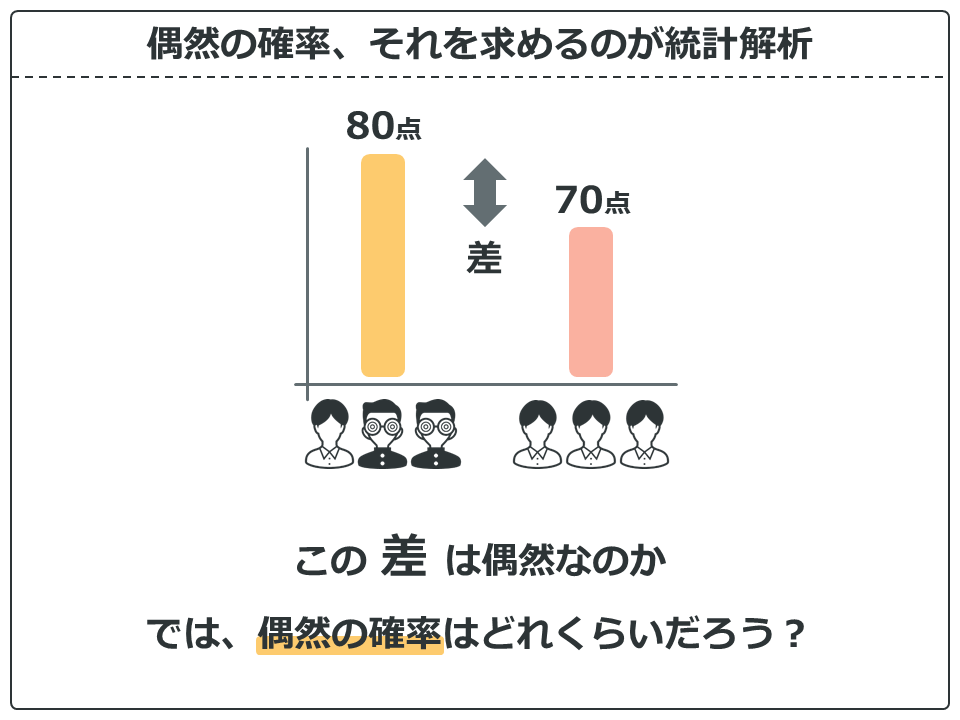
1組と2組の3人のテストの平均点をグラフにしてみました。差は10点あります。この10点の差は、たまたまこの3人を選んだことによる偶然なのでしょうか?
「たまたま」や「偶然」という言葉って、「何回かの行動の中で起きたこと」ですよね。例えば「ホームランを打てたのは偶然だよ」は「100回打った中でホームランが1回」というような時に使います。100回中1回、言い換えると1%の確率ですよね。つまり「偶然」は「確率」として捉えることができます。
偶然の確率、それを求めるのが統計解析ということです。
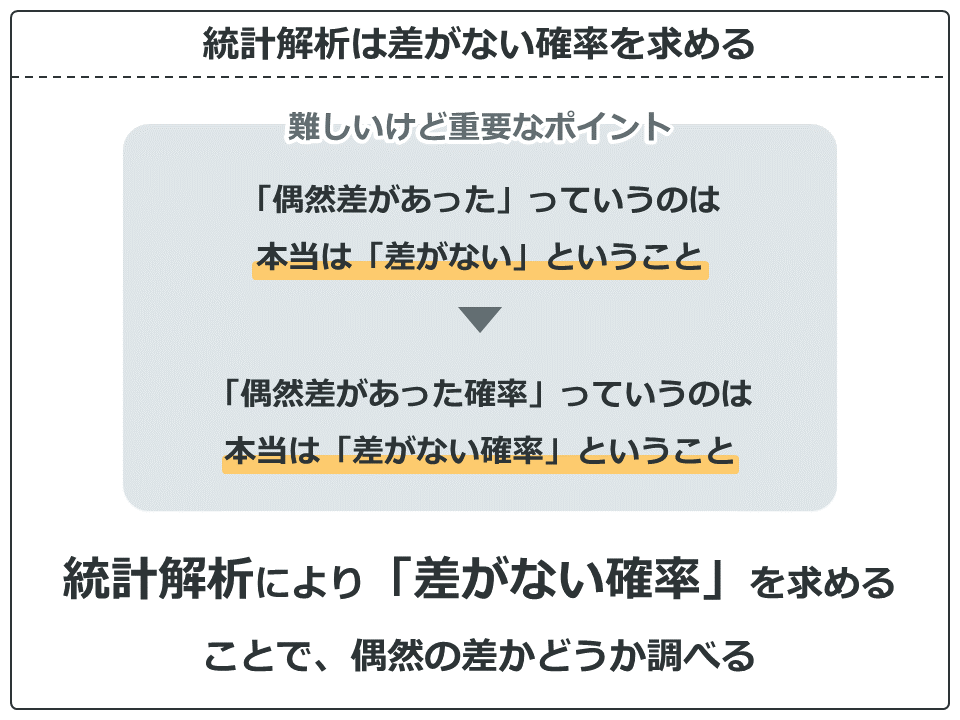
ここが今回の記事で一番難しいところ。むしろ統計解析を学ぶ上で一番難しいところかもしれません。何回も読み返して理解してください。
「偶然差があった」ということは、本当は「差がない」ということです。つまり、「偶然差があった確率」というのは、本当は「差がない確率」ということになります。これ以上かみ砕いて説明するすべが私にはないので、頑張って理解してください。
統計解析は「偶然の確率」を求めるといいましたが、厳密には「差がない確率」を求める方法になります。今回はこれ以上深く考えなくて大丈夫ですが、後々大事なことなので、なんとなく理解しておくといいと思います。
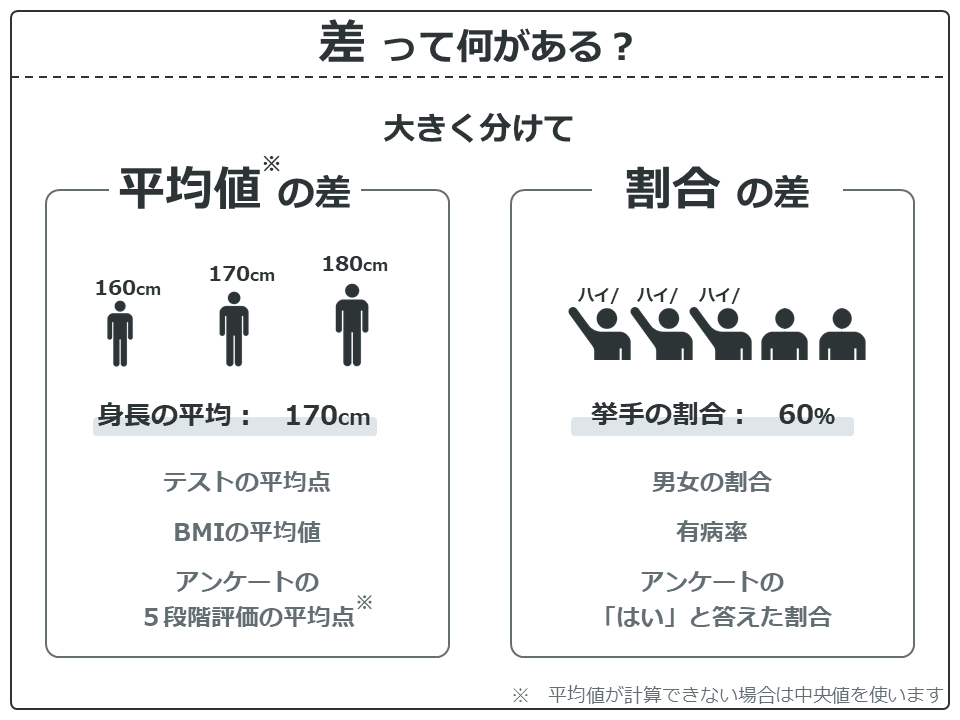
では、統計解析で調べることのできる「差」には何があるでしょうか?
大きく分けて「差」には、平均値の差と割合の差があります。平均値が計算できない場合は中央値という値を使うことがありますが、それは追々説明します。
平均値の差にはテストやBMIがあります。割合の差はちょっとだけわかりにくいですが、例えば男性の割合が1組は50%、2組は60%の場合、この10%の差のことです。他にも有病率やアンケートで「はい」と答えた割合なんかも差を求めることができますね。
下の例は、より現実的な例を出してみたので、なんとなくでいいのでイメージを沸かしてください。
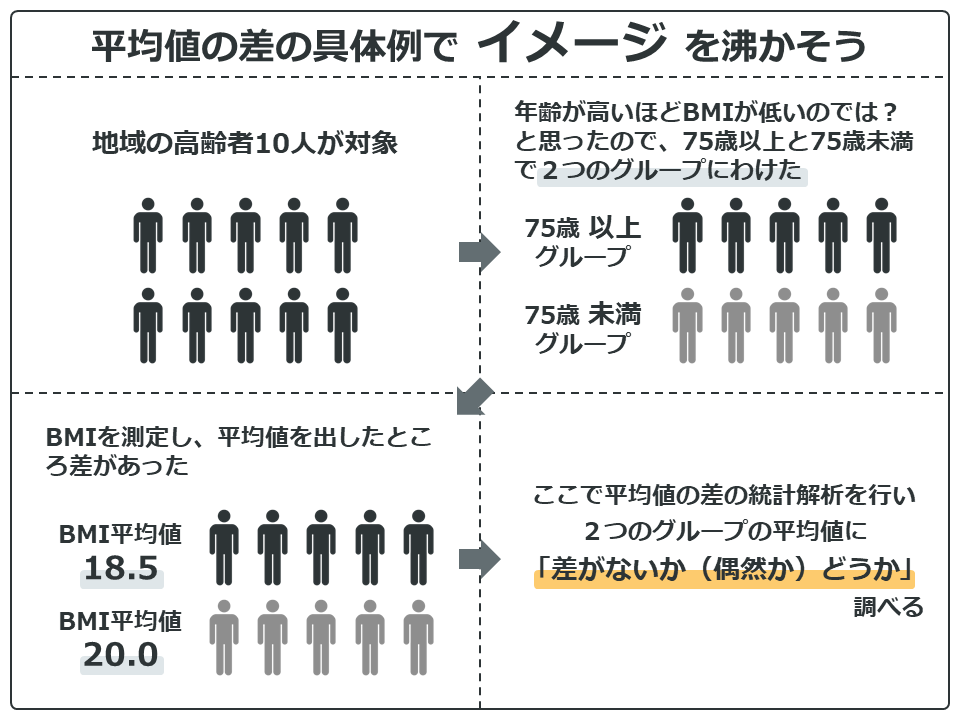
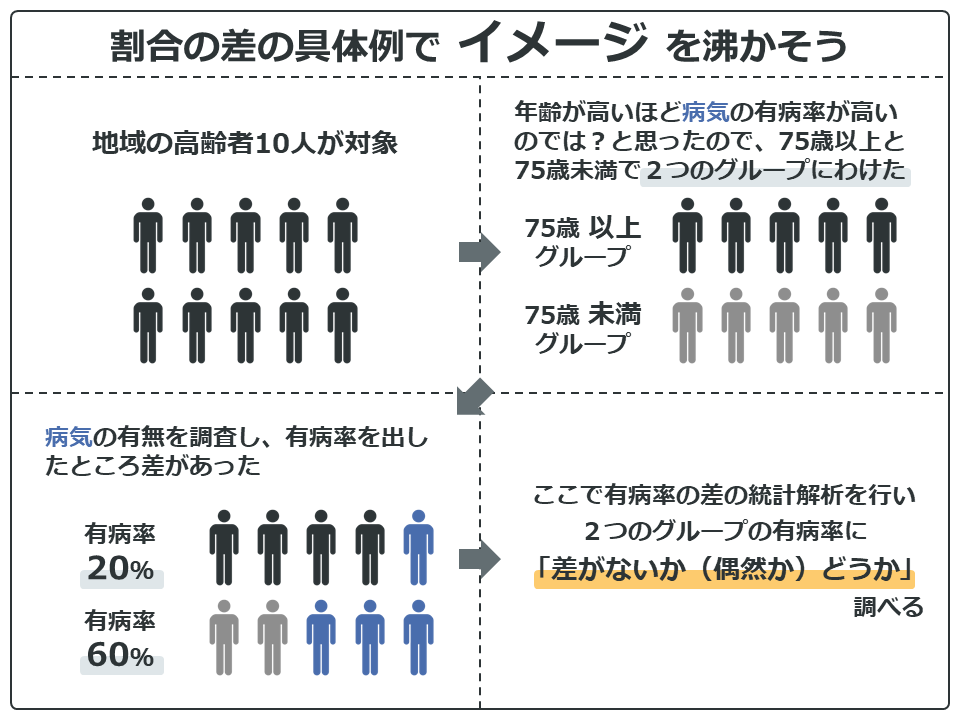
ちょっとポイントですが、差をみているので必ず2つ(以上)のグループを比較することになります。
このように統計解析では、2つ(以上)のグループ間の、平均値や割合に「差がないか(偶然か)どうか」調べることができます。
実はほとんどの統計解析はこれだけしかできないんですね。なのでこれだけできるようになれば、ほとんどの統計解析ができるようになったようなものです。高度な統計も、このような考え方がもとになっているのです。
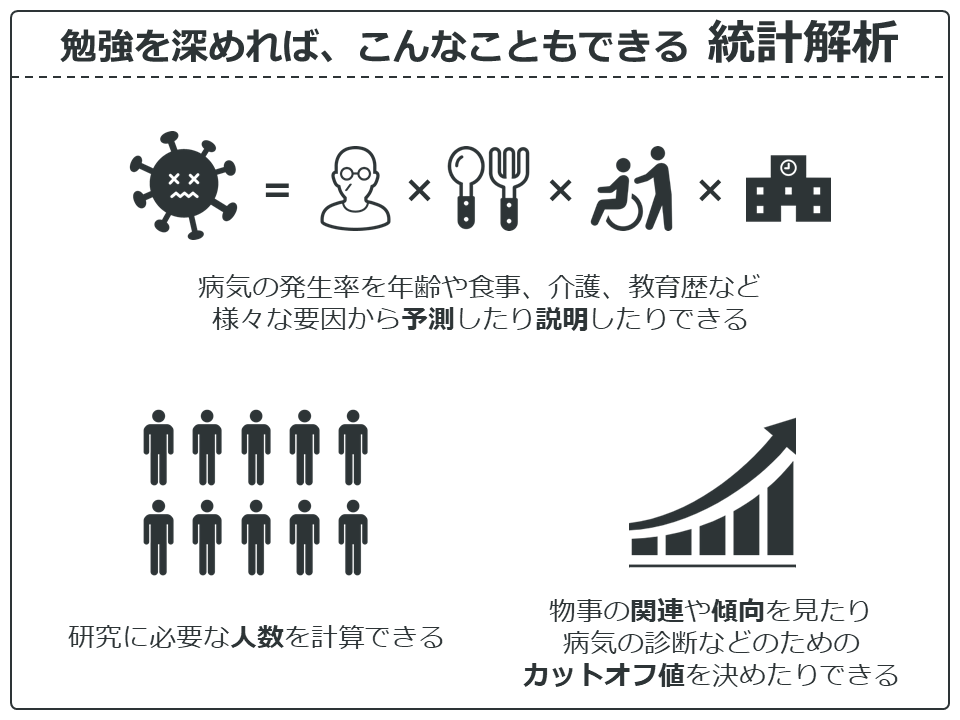
統計解析の勉強を深めていけば、このようなこともできるようになります。もちろんこのブログでも紹介していくので、また参考にしてください。
- 2つ(以上)のグループ間の、平均値や割合に「差がないか(偶然か)どうか」調べることができる
まとめ(時間がない人はココだけ)
- 統計解析の原理は知らなくてもなんとかなる
- 事故らないために最低限のルールは覚える
- 統計解析は2つ(以上)のグループ間の、平均値や割合に「差がないか(偶然か)どうか」調べることができる