ふっふっふ

ど、どうしたんですか?

t検定を覚えたんで、たくさんの群を一緒に比較しまくっているんです

それ、だめですよ

…え?

それ、ダメですよ(2回目)
3群以上の比較には特別な方法を使おう
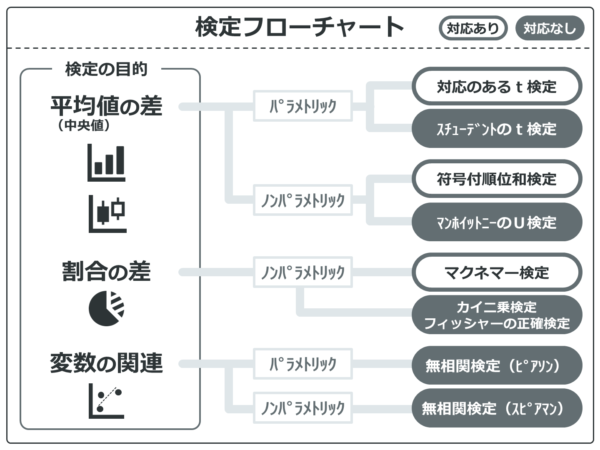
3群以上の比較を行うには、スチューデントのt検定や符号付順位和検定、フィッシャーの正確検定といった基本的な統計手法を覚えておく必要があります。基本的な統計手法は下記関連記事を参考にしてください。

さて、基本的な統計手法では2つのグループを比較していましたが、世の中には3つ以上に分かれることだってあります。
このように3つ以上のグループにおいて、平均値や中央値、割合といった値を比較するにはどうすればいいでしょうか?
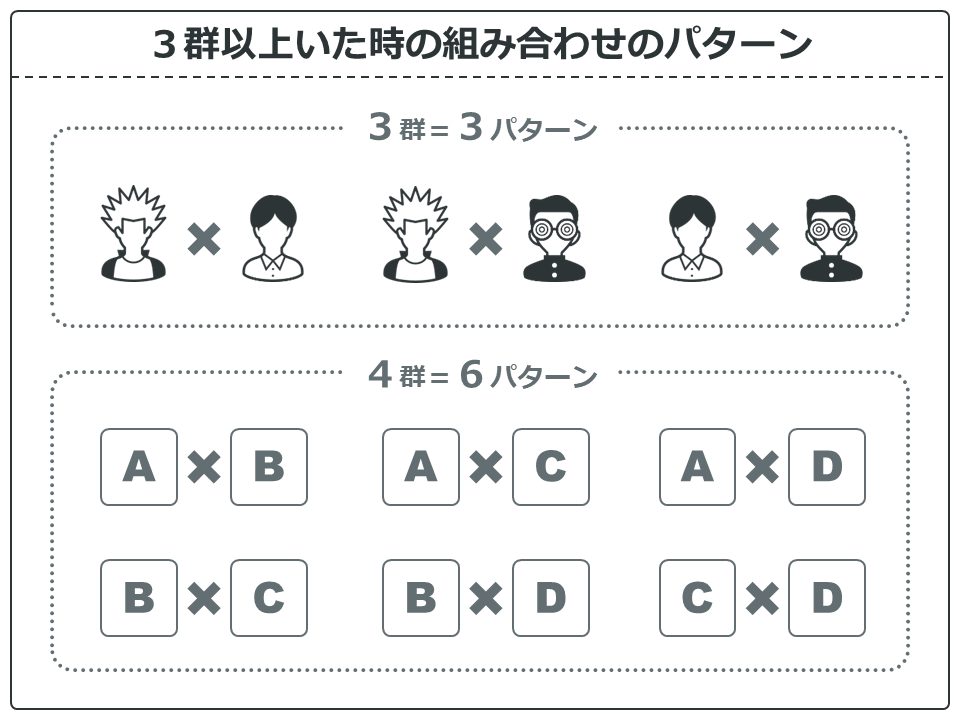
すでにスチューデントのt検定やフィッシャーの正確検定のような2群間の比較ができるのであれば、各組み合わせで検定を繰り返せばできそうな気がします…。
例えば3群であれば3パターンの組み合わせがあるので、2群間比較を3回行う。4群であれば全部で6回行えばすべての組み合わせを比較できるような気がします。

でも、この方法はダメなんです。
まず、必ず覚えてほしいことがあります。それは…
3群以上の比較の場合、2群間比較の検定を繰り返してはいけない!ということです。
3群以上の比較には、特別な検定手法を用いることになります。
なぜ3群以上の比較には特別な方法が必要なの?
では、特別な検定手法の詳細を紹介する前に、なぜなぜ3群以上の比較には特別な方法が必要なのかみていきましょう。

まずはP値と有意水準について、おさらいしましょう。
P値とは検定結果が間違っている確率です。そして有意水準は、その間違いをどこまで許してあげるかの基準です。
有意水準5%(P<0.05)とは、検定を100回やったら95回は正しいけど5回は間違えるよってこと。まぁ5回なら偶然ってことにしてあげるよってことです。
さて、確率の問題です。
正しい確率が95%のことを3回やって、全部正しい確率っていくつになるかわかりますか?

正しい確率が95%を3回やるということは、0.95×0.95×0.95で計算できます(そういうもんです)。
つまり、正しい確率が95%のことを3回やって 全部、正しい確率は85.7%になるんですね。
裏を返せば、3回やって少なくとも1回以上間違っている確率は14.3%になります。
あれ?やばくないですか?有意水準は5%なので、5%までは偶然ってことにして大目に見てましたが、14.3%も間違っている確率があるのであれば、ちょっと許容できないですよ!!
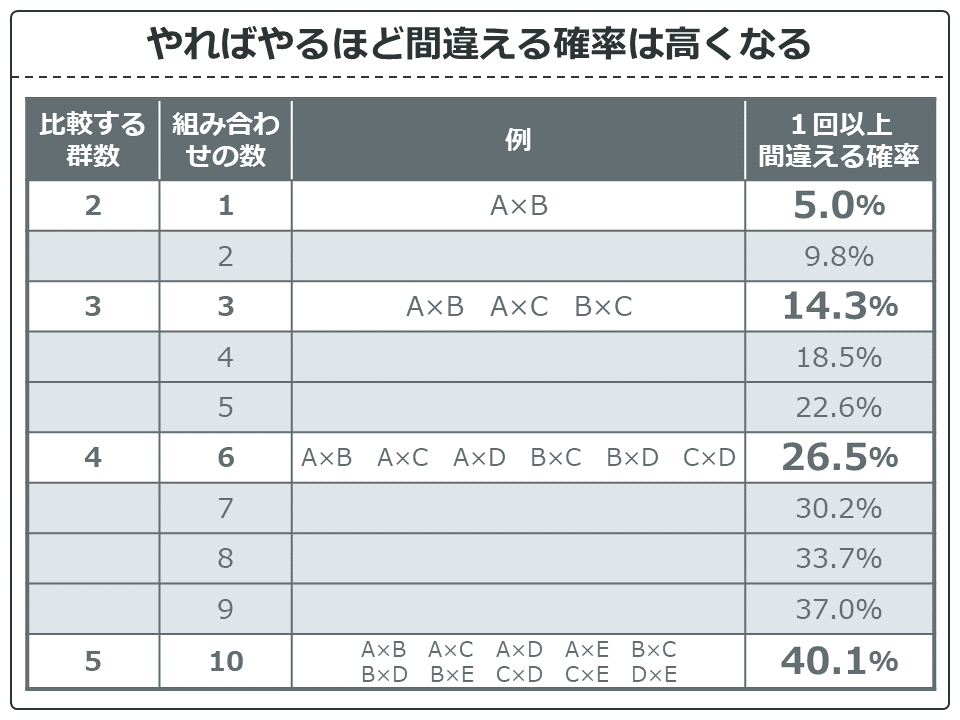
実は、有意水準5%で検定をやればやるほど間違える確率は高くなっていきます。
比較する群が2群の時は、組み合わせは1つしかないので、1回以上間違える確率は5%でした。これが有意水準5%ということです。
でも、3群では14.3%に、4群では26.5%、5群にいたっては組み合わせが10パターンになり、1回以上間違える確率も40.1%とすさまじことになってしまっています。
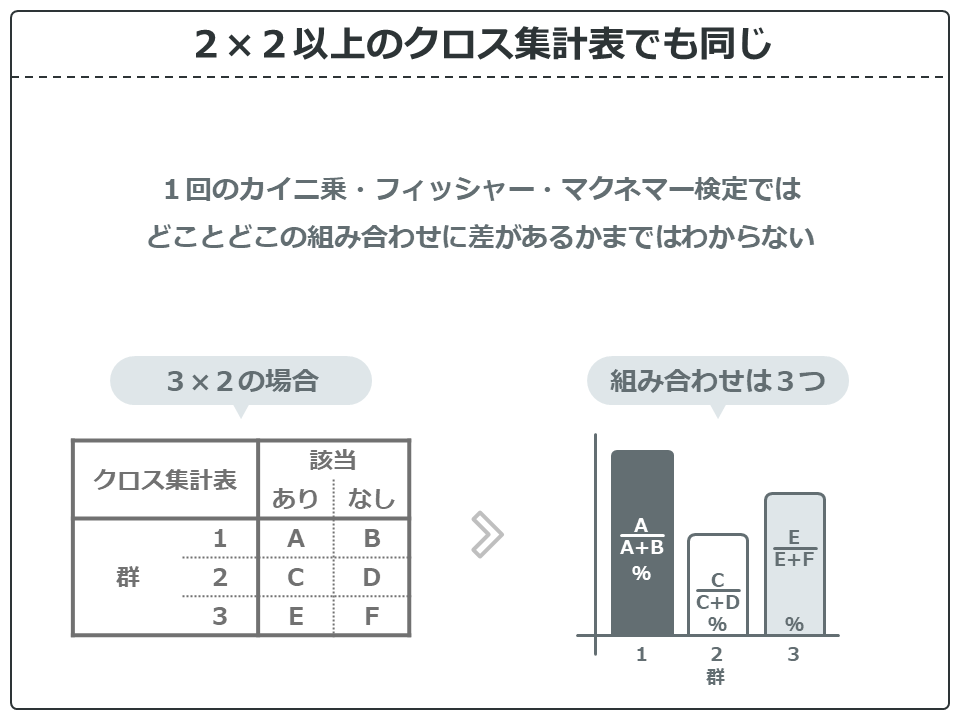
これは2×2以上のクロス集計表でも同じことになります。
その他、対応のある検定で【過去】【現在】【未来】の3時点で比較しても、同じような問題が発生します。
この検定の繰り返しによる間違える確率の増大問題を解決するために、3群以上または3時点以上の比較には特別な検定手法が必要になってくるんですね。
3群以上または3時点以上の比較の方法
それでは3群以上または3時点以上の比較方法について見ていきましょう。
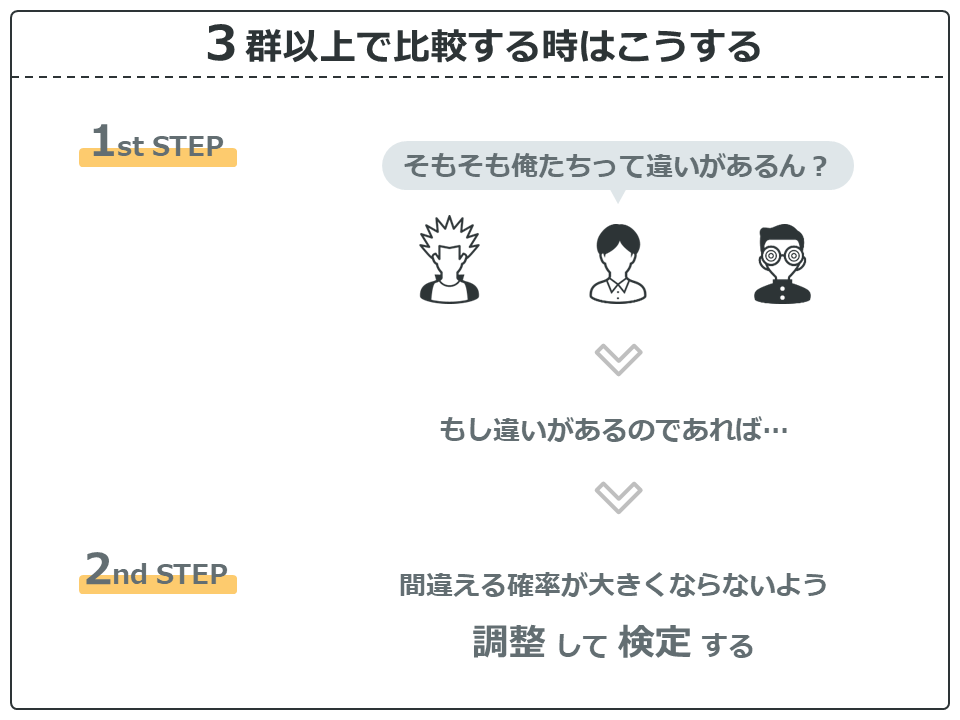
3群以上の比較を行う場合は2stepに分かれて検定を行います。
1st stepは、全体で見ます。全体のどこかに違いがあるかを検定していくことになります。
2nd stepは、1st stepでもし違いがあれば、繰り返しの検定により間違える確率が大きくならないよう調整しながら、どことどこに差があるかを検定していきます。
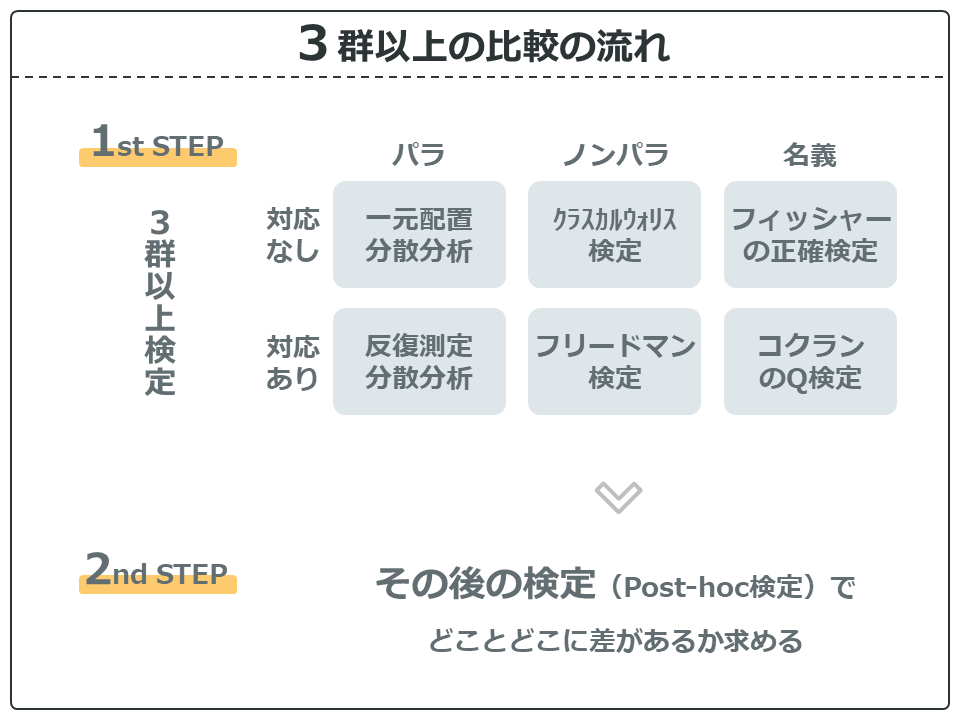
では、具体的に見ていきましょう。
1st stepでは、対応あり・なし、パラメトリック・ノンパラメトリック、名義尺度の検定により検定手法が分かれています。この検定ではP値は1つしか出ません。このP値が0.05(5%)未満であれば、全体の中のどこかに差があることがわかります。
全体の中のどこかに差があるかがわかれば、2nd stepでどことどこに差があるかを求めます。これをその後の検定(Post-hoc検定)や多重比較検定と呼びます。
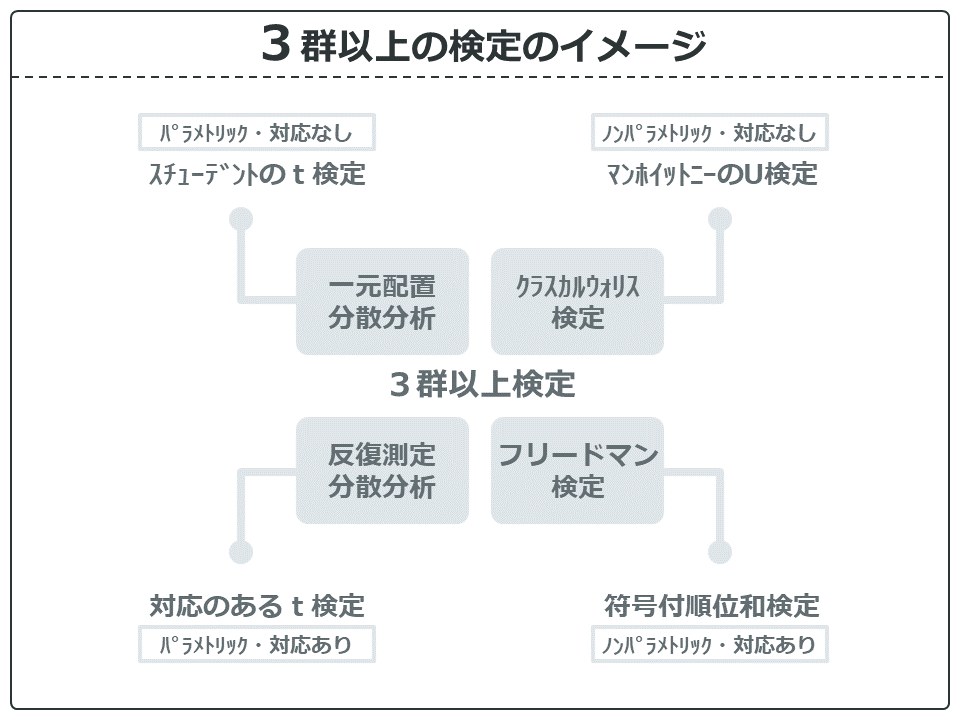
2群間の比較を行う基本的な統計と3群以上の検定の関係のイメージ図です。
例えば、一元配置分散分析は、パラメトリックで対応のない2群間の平均値の比較のスチューデントのt検定の3群以上バージョンのようなものです。
新しい統計の名前が色々出てきて、うげぇってなるかもしれませんね。
でも、クラスカル・ウォリス検定はマンホイットニーのU検定、反復測定分散分析は対応のあるt検定、フリードマン検定は符号付順位和検定の3群または3時点以上バージョンだと思えば、そんなに難しくないんじゃないですか?
ちなみに、フィッシャーの正確検定は3群以上でも使えるので、3群以上でもフィッシャーの正確検定です。マクネマー検定の3時点以上バージョンがコクランのQ検定にあたります。
どことどこに差があるかその後の検定を使おう
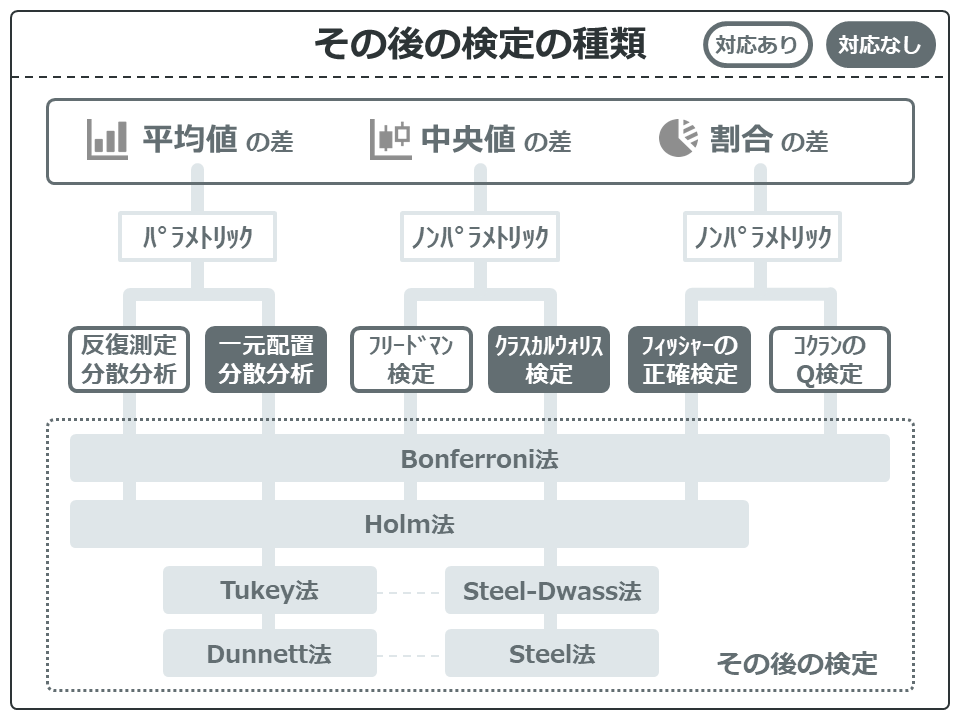
3群以上または3時点以上の比較方法と、それぞれのその後の検定の種類を図にまとめました。
新しい名前がいっぱいですね…。
順番に見ていきましょう!
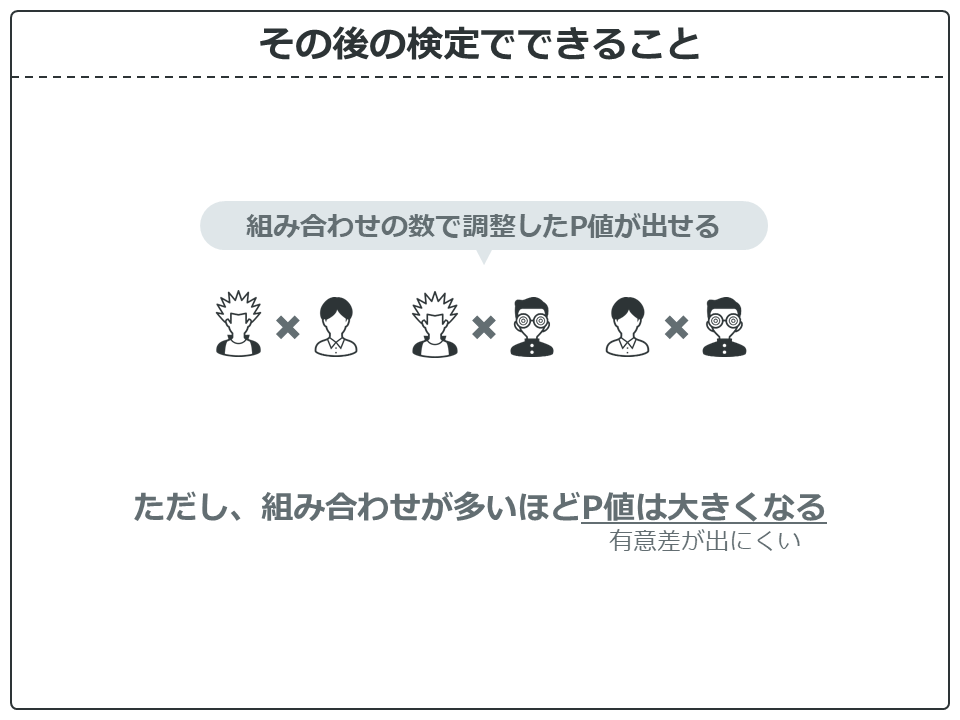
まず、その後の検定でできることを確認しておきましょう、
その後の検定では、どことどこに差があるか調べるために、組み合わせの数で調整したP値を求めることができます。
ただし、組み合わせが多いほどP値は大きくなる=つまり有意差が出にくくなります。5群以上になると、かなりの人数がいるか、はっきりとした差がないと有意差が出にくくなります。
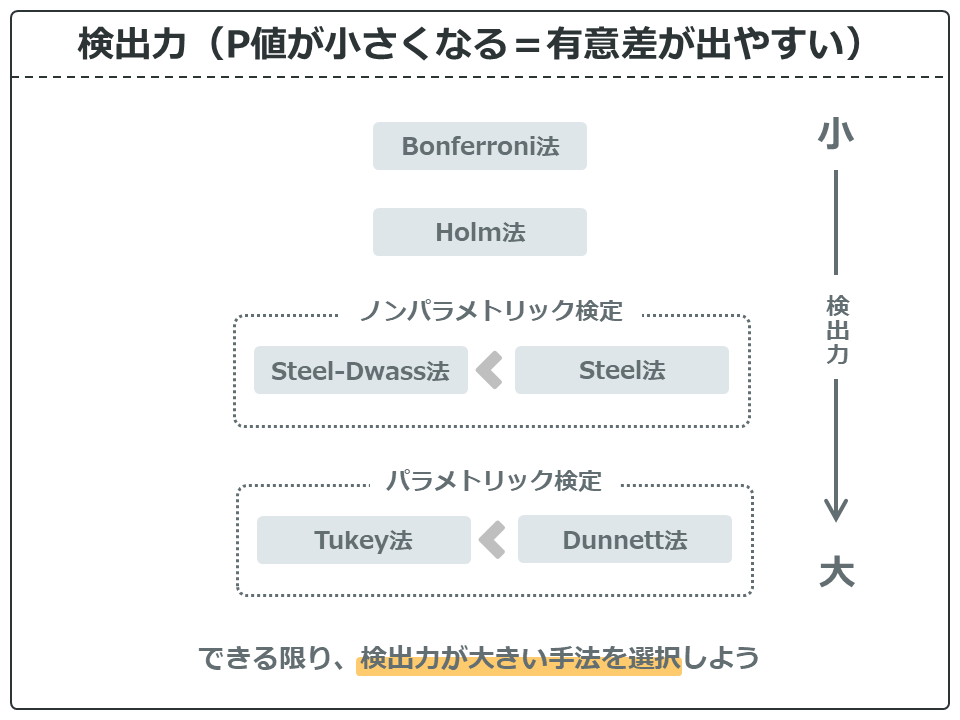
差を見つける力を検出力といいます。簡単に言えば、どの方法がP値が小さくなるかということですね!
とりあえず、Bonferroni法(ボンフェローニ法)は、簡単に計算できてどの手法でも使えるけど、有意差が出にくい方法ということを覚えておきましょう。ただ、簡単なので結構論文とかにも使われたりしています。
それぞれの手法の記事で、おすすめのその後の検定を紹介しているので、ここでは深く考えなくてOKです。
ただ、Steel法とDunnett法だけは、使い方が少し違うので、最後にそこだけ確認しておきましょう。
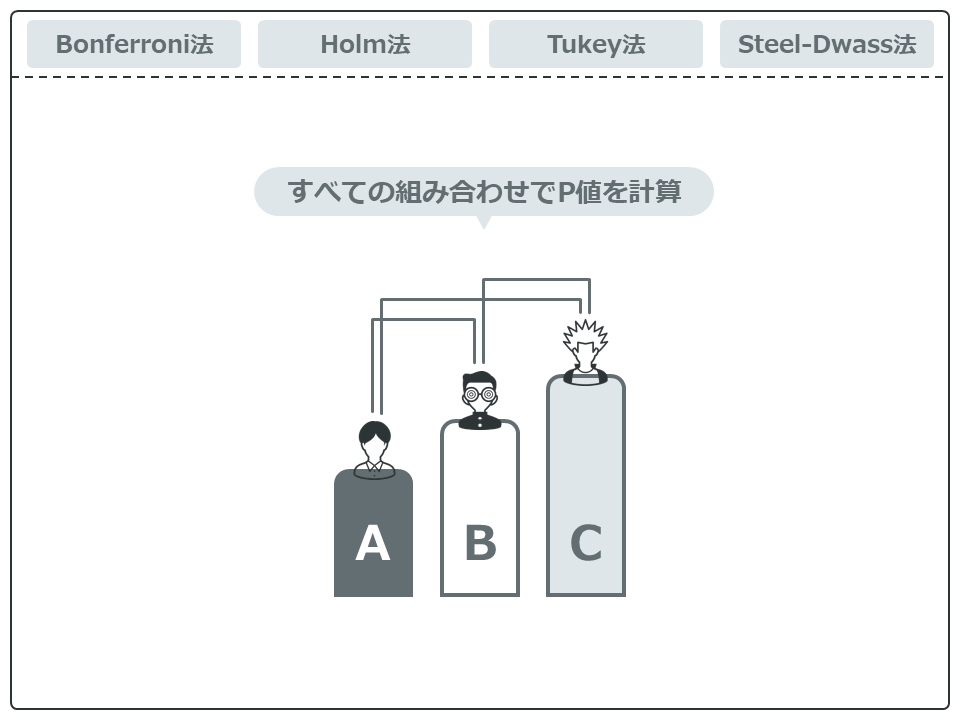
まず、Bonferroni法、Holm法、Tukey法、Steel-Dwass法です。これは、すべての組み合わせでP値を計算します。
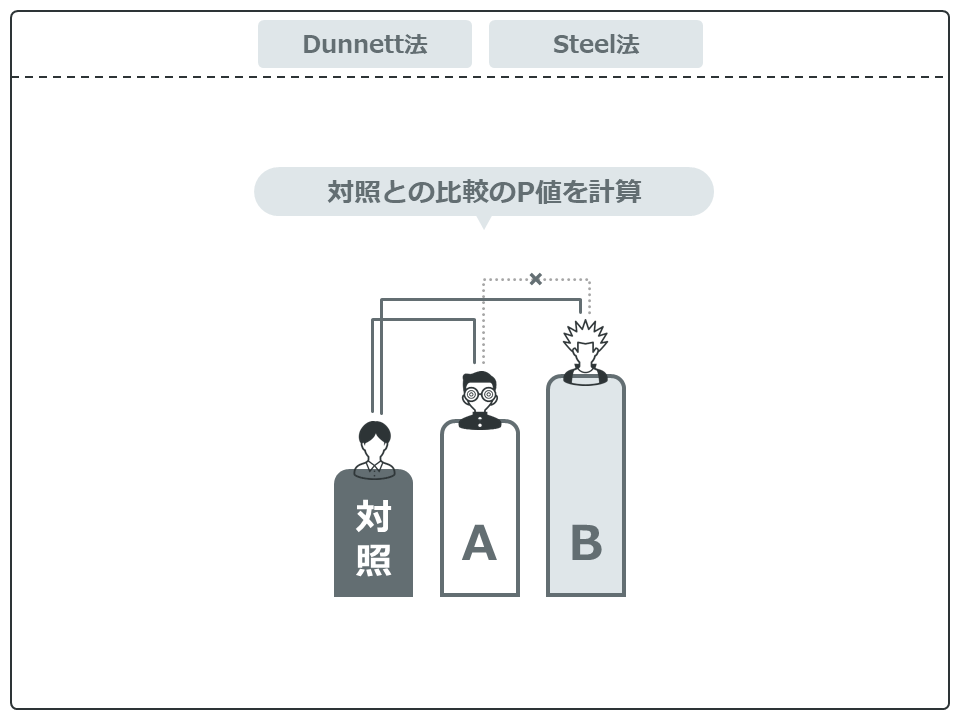
それに対し、Dunnett法とSteel法は対照群を1つ決めて、そことの差を検定します。上の図の例では、【対照×A】と【対照×B】のみ検定し、【A×B】は検定しません。
そのため組み合わせの数が減り、P値が小さくなりやすいです(有意差が出やすい)。
もちろん、P値が小さくなるので使うのではなく、研究の目的として【A×B】が必要ない場合に使うようにしましょうね!
まとめ(時間のない人はココだけ)
3群または3時点以上の検定は専用の検定手法を用いる
- 一元配置分散分析
- クラスカル・ウォリス検定
- 反復測定分散分析
- フリードマン検定
- フィッシャーの正確検定
- コクランのQ検定
また、EZRで行う3群以上の検定を含む高度な統計解析の方法は下記カテゴリーから学べます。